Non-Right Triangle Trigonometry

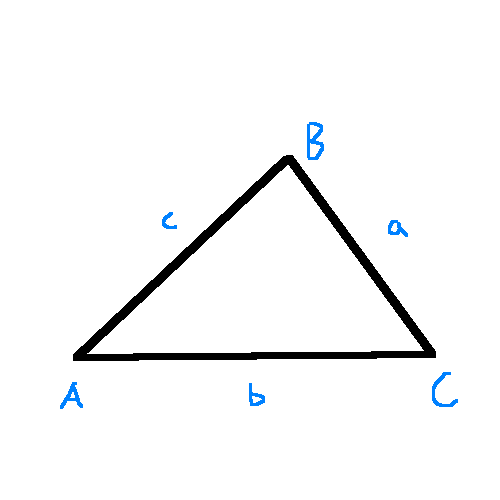
Below are a few laws that help with finding sides and angles for non right triangles. We will use the standard triangle $\Delta ABC$ with sides $a$, $b$, and $c$ being opposite of their respective angles.

The law of sines is the most simple of the trig laws, however there are some edge cases you must worry about.

• $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

When solving for an angle on an ASS¹⁾ triange, there can be two solutions, and thus two triangles. To get the other angle, subtract the calculated one by 180 degrees and check if it makes a valid triangle that doesn't have angle measures > 180. Sometimes there can also be no solution if your calculator spits out a domain error.

While the law of cosine seems difficult to remember, it is actually just Pythagorean theorem with an angle correction.

• $c^2 = a^2 + b^2 - 2ab\cos C$

With this angle correction, you can actually swap $a$, $b$, and $c$ around solong as you keep the $c$ and $C$ angle pair of the original equation. So, the following are actually also valid:

• $a^2 = b^2 + c^2 - 2bc\cos A$
• $b^2 = a^2 + c^2 - 2ac\cos B$

check if the ASA thing is true or not.

The formula is just the standard triangle area equation with a $\sin$ added.

• $\text{area} = \frac{1}{2}bc\sin A$

The variables can be swapped around just like in Law of Cosine, but the triangle NEEDS to be an ASA²⁾ triangle for this to work.

The Law of Cosines can be used to establish the following formula for the area of a triangle. You can use it for any SSS³⁾ triangle.

• $\text{area} = \sqrt{s(s-a)(s-b)(s-c)}$ where $s = \frac{a + b + c}{2}$