This is an old revision of the document!
Table of Contents
Limits
A limit is the y-value of a function as it approaches a certain value. As a function arbitrarily approaches the corresponding x-value of a limit, the function output also gets arbitrarily closer to the limit itself. Note that limits do not necessarily mean that the value is a discontinuity, there are both continuous and non-continuous limits. Limits do not necessarily have to exist on the function.
Types of limits
- $\frac{n_1}{n_2}$ || $\frac{0}{n}$
Indeterminate
If a rational function, when plugging in a discontinuity1), evaluates to $\frac{0}{0}$, it is called an indeterminate. To solve for the discontinuity, one must simplify away the denominator which causes the discontinuity2). When finding limits of indeterminates, use Polynomial Division3) or factoring to simplify. Any factors removed are called removable discontinuities4). You can use the simplified function to find the limit.
Undefined
When evaluating a function that results in a divide by zero, specifically $\frac{1}{0}$, it's result is undefined. These types of functions are easy to tell as they clearly approach infinity when graphed. However, infinity is not a number, it is a concept, As such, the limit for this function Does Not Exist.
Piecewise
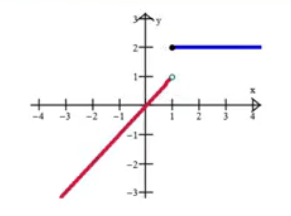With a function like this, where both sides approach different values, the limit also Does Not Exist. Both sides must approach the same y-value for a limit to exist.
