Limits

A limit is the y-value of a function as it approaches a certain value. As a function arbitrarily approaches the corresponding x-value of a limit, the function output also gets arbitrarily closer to the limit itself. Note that limits do not necessarily mean that the value is a discontinuity, there are both continuous and non-continuous limits. Limits do not necessarily have to exist on the function.

Types of limits

• $\frac{n_1}{n_2}$ || $\frac{0}{n}$ are both valid
• $\frac{n}{0}$ is undefined
• $\frac{0}{0}$ is indeterminate

If a rational function, when plugging in a discontinuity¹⁾, evaluates to $\frac{0}{0}$, it is called an indeterminate. To solve for the discontinuity, one must simplify away the denominator which causes the discontinuity²⁾. When finding limits of indeterminates, use Polynomial Division³⁾ or factoring to simplify. Any factors removed are called removable discontinuities⁴⁾. You can use the simplified function to find the limit.

When evaluating a function that results in a divide by zero, specifically $\frac{1}{0}$, it's result is undefined. These types of functions are easy to tell as they clearly approach infinity when graphed. However, infinity is not a number, it is a concept, As such, the limit for this function Does Not Exist.

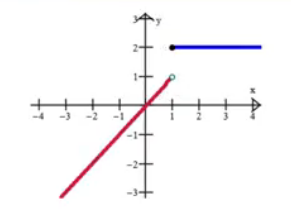With a function like this, where both sides approach different values, the limit also Does Not Exist. Both sides must approach the same y-value for a limit to exist.

As x approaches $\infty$ or $-\infty$, x will approach the ratio of the leading coefficents⁵⁾.