Table of Contents
Derivative
The derivative of a function (say $f(x)$) is a function of the slope of the tangent line at any given point. It is a generic slope formula for any x value, or instantaneous rate of change. The output of the derivative can be used to make tangent lines. Its notation is $f'(x)$ or $\frac{d}{dx} f(x)$.
When is a Derivative Valid?
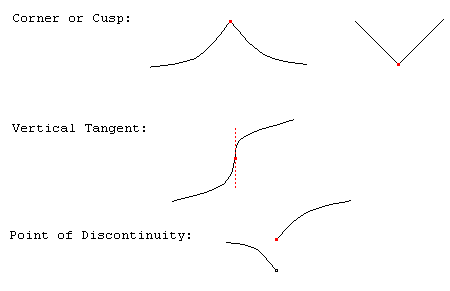
A derivative is valid when the function is continuous and when it is differentiable, meaning that both sides of a function approaches the same slope at any given point. If not, this means that there is either a cusp, corner, or vertical tangent present.
- A cusp is present when each side of a function approaches a vertical slope, which Does Not Exist.
- A corner is present when there is a sharp change in slope, which prevents a continuous derivative.
- A vertical tangent means that each side of the slope function approaches infinity from a different direction.
- A discontinuity means that the slope function is also has a discontinuity, which prevents a continuous derivative.
Calculating the Derivative
Using the slope formula $m = \frac{y_2-y_1}{x_2-x_1}$, you can derive the definition of a derivative using a limit.
$$ \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} = f'(x) $$
The idea is to use a limit to get the instantaneous rate of change of a function as $h$ or the difference between $x_2$ and $x_1$ becomes indefinitely small. Basically get the slope from two points, but the two points are indefinitely close to eachother, or basically one point, which is the slope of a tangent line!
Using the Alternative Form
Using the definition of a derivative is a pain in the ass. There is an alternative definition using the same slope formula for the slope at one specific point that you can use instead if you don't need the derivative function.
$$ \lim_{x \to a} \frac{f(x) - f(a)}{x - a} = f'(a) $$
- $a$ is the point where you wish to find the tangent line
This is much simpler to compute, however it only works for the one value $a$. Don't mix it up and think you can plug in any value once you simplify to get the slope at any point!
This Sucks I Want Out!
No worries! Calculating limits is hard, that's why there are rules to save yourself time when calculating derivatives. Hopefully you'll never have to use the definition of a derivative to find it.